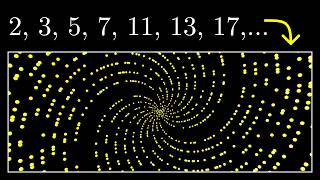
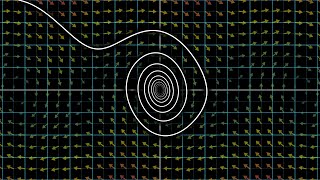
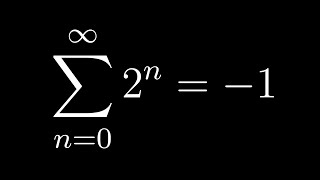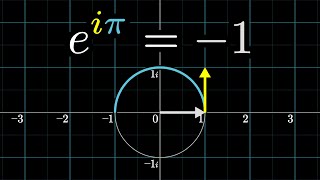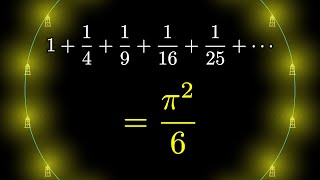Why do prime numbers make these spirals? | Dirichlet’s theorem and pi approximations |

|
|
A curious pattern, approximations for pi, and prime distributions.
Help fund future projects: https://www.patreon.com/3blue1brown An equally valuable form of support is to simply share some of the videos. Special thanks to these supporters: http://3b1b.co/spiral-thanks Based on this Math Stack Exchange post: https://math.stackexchange.com/questions/885879/meaning-of-rays-in-polar-plot-of-prime-numbers/885894 Want to learn more about rational approximations? See this Mathologer video. https://youtu.be/CaasbfdJdJg Also, if you haven't heard of Ulam Spirals, you may enjoy this Numberphile video: https://youtu.be/iFuR97YcSLM Dirichlet's paper: https://arxiv.org/pdf/0808.1408.pdf Timestamps: 0:00 - The spiral mystery 3:35 - Non-prime spirals 6:10 - Residue classes 7:20 - Why the galactic spirals 9:30 - Euler’s totient function 10:28 - The larger scale 14:45 - Dirichlet’s theorem 20:26 - Why care? Corrections: 18:30: In the video, I say that Dirichlet showed that the primes are equally distributed among allowable residue classes, but this is not historically accurate. (By "allowable", here, I mean a residue class whose elements are coprime to the modulus, as described in the video). What he actually showed is that the sum of the reciprocals of all primes in a given allowable residue class diverges, which proves that there are infinitely many primes in such a sequence. Dirichlet observed this equal distribution numerically and noted this in his paper, but it wasn't until decades later that this fact was properly proved, as it required building on some of the work of Riemann in his famous 1859 paper. If I'm not mistaken, I think it wasn't until Vallée Poussin in (1899), with a version of the prime number theorem for residue classes like this, but I could be wrong there. In many ways, this was a very silly error for me to have let through. It is true that this result was proven with heavy use of complex analysis, and in fact, it's in a complex analysis lecture that I remember first learning about it. But of course, this would have to have happened after Dirichlet because it would have to have happened after Riemann! My apologies for the mistake. If you notice factual errors in videos that are not already mentioned in the video's description or pinned comment, don't hesitate to let me know. Thanks to these viewers for their contributions to translations Hebrew: Omer Tuchfeld ------------------ These animations are largely made using manim, a scrappy open-source python library: https://github.com/3b1b/manim If you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind. Music by Vincent Rubinetti. Download the music on Bandcamp: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown Stream the music on Spotify: https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5u If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people. ------------------ 3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribe Various social media stuffs: Website: https://www.3blue1brown.com Twitter: https://twitter.com/3blue1brown Reddit: https://www.reddit.com/r/3blue1brown Instagram: https://www.instagram.com/3blue1brown_animations/ Patreon: https://patreon.com/3blue1brown Facebook: https://www.facebook.com/3blue1brown |